Lösning:
Uppg. a
I mitten av de femuddiga stjärnorna finns en regelbunden femhörning.
Vinklarna i en sådan femhörning är 108^o. Då är det lätt att räkna ut att vinkeln i en "stjärnudd" är 36^o.

Lösning:
Uppg. b
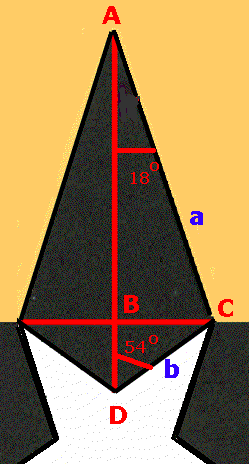
Areaskalan = (längdskalan)²

Om vi kan jämföra sträckan AC (a) i den svarta stjärnan med motsvarande sträcka CD (b) i den vita stjärnan så kan vi lösa problemet.
Elementär trigonometri ger:
Sträckan BC = a sin 18^o
Sträckan CD (b)= a sin 18^o /sin 54^o

Alt. 1: Längdskalan sin 18^o /sin 54^o  kan beräknas med miniräknare.
sin 18^o /sin 54^o  ≈ 2,618
Areaskalan ≈ 2,618² = 6,854
Alt. 2: sin 18^o =
Utnyttja formeln

Då får man efter förenkling
Längdskalan:sin 54^o/sin 18^o =
Areaskalan = (längdskalan)²

Areaskalan:
()² =   ≈  6,854
Anm.: Lösningen kan också skrivas
(φ + 1)²
(φ = 1,618... Se Gyllene snittet)
 

Henrich Hemme har i sin bok "Die Hölle der Zahlen" en variant av detta problem med en lösning  utan trigonometri.